1 – Introdução
Chama-se experimento aleatório àquele cujo resultado é imprevisível, porém pertence necessariamente a um conjunto de resultados possíveis denominado espaço amostral.
Qualquer subconjunto desse espaço amostral é denominado evento.
Se este subconjunto possuir apenas um elemento, o denominamos evento elementar.
Por exemplo, no lançamento de um dado, o nosso espaço amostral seria U = {1, 2, 3, 4, 5, 6}.
Exemplos de eventos no espaço amostral U:
A: sair número maior do que 4: A = {5, 6}
B: sair um número primo e par: B = {2}
C: sair um número ímpar: C = {1, 3, 5}
Nota: O espaço amostral é também denominado espaço de prova.
Trataremos aqui dos espaços amostrais equiprováveis, ou seja, aqueles onde os eventos elementares possuem a mesma chance de ocorrerem.
Por exemplo, no lançamento do dado acima, supõe-se que sendo o dado perfeito, as chances de sair qualquer número de 1 a 6 são iguais. Temos então um espaço equiprovável.
Qualquer subconjunto desse espaço amostral é denominado evento.
Se este subconjunto possuir apenas um elemento, o denominamos evento elementar.
Por exemplo, no lançamento de um dado, o nosso espaço amostral seria U = {1, 2, 3, 4, 5, 6}.
Exemplos de eventos no espaço amostral U:
A: sair número maior do que 4: A = {5, 6}
B: sair um número primo e par: B = {2}
C: sair um número ímpar: C = {1, 3, 5}
Nota: O espaço amostral é também denominado espaço de prova.
Trataremos aqui dos espaços amostrais equiprováveis, ou seja, aqueles onde os eventos elementares possuem a mesma chance de ocorrerem.
Por exemplo, no lançamento do dado acima, supõe-se que sendo o dado perfeito, as chances de sair qualquer número de 1 a 6 são iguais. Temos então um espaço equiprovável.
Em oposição aos fenômenos aleatórios, existem os fenômenos determinísticos, que são aqueles cujos resultados são previsíveis, ou seja, temos certeza dos resultados a serem obtidos.
Normalmente existem diversas possibilidades possíveis de ocorrência de
um fenômeno aleatório, sendo a medida numérica da ocorrência de cada uma
dessas possibilidades, denominada Probabilidade.
Consideremos uma urna que contenha 49 bolas azuis e 1 bola branca. Para
uma retirada, teremos duas possibilidades: bola azul ou bola branca.
Percebemos entretanto que será muito mais frequente obtermos numa
retirada, uma bola azul, resultando daí, podermos afirmar que o evento
"sair bola azul" tem maior probabilidade de ocorrer, do que o evento
"sair bola branca".
2 – Conceito elementar de Probabilidade
Seja U um espaço amostral finito e equiprovável e A um determinado
evento ou seja, um subconjunto de U. A probabilidade p(A) de ocorrência
do evento A será calculada pela fórmula
p(A) = n(A) / n(U)
onde:
n(A) = número de elementos de A e n(U) = número de elementos do espaço de prova U.
Vamos utilizar a fórmula simples acima, para resolver os seguintes exercícios introdutórios:
p(A) = n(A) / n(U)
onde:
n(A) = número de elementos de A e n(U) = número de elementos do espaço de prova U.
Vamos utilizar a fórmula simples acima, para resolver os seguintes exercícios introdutórios:
1.1 - Considere o lançamento de um dado. Calcule a probabilidade de:
a) sair o número 3:
Temos U = {1, 2, 3, 4, 5, 6} [n(U) = 6] e A = {3} [n(A) = 1]. Portanto, a probabilidade procurada será igual a p(A) = 1/6.
Temos U = {1, 2, 3, 4, 5, 6} [n(U) = 6] e A = {3} [n(A) = 1]. Portanto, a probabilidade procurada será igual a p(A) = 1/6.
b) sair um número par: agora o evento é A = {2, 4, 6} com 3 elementos; logo a probabilidade procurada será p(A) = 3/6 = 1/2.
c) sair um múltiplo de 3: agora o evento A = {3, 6} com 2 elementos; logo a probabilidade procurada será p(A) = 2/6 = 1/3.
d) sair um número menor do que 3: agora, o evento A = {1, 2} com dois elementos. Portanto,p(A) = 2/6 = 1/3.
e) sair um quadrado perfeito: agora o evento A = {1,4} com dois elementos. Portanto, p(A) = 2/6 = 1/3.
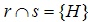. Sendo que H está contido na reta r e na reta s.